Models for the threat of AI

Tyler Cowan, on Russ Roberts’ podcast EconTalk in early 2023, spoke of the lack of models that might explain how exactly AI might pose an existential risk to humanity:

So, if you look, say, at COVID [corona virus disease] or climate change fears, in both cases, there are many models you can look at, including--and then models with data. I'm not saying you have to like those models. But the point is: there's something you look at and then you make up your mind whether or not you like those models; and then they're tested against data. So, when it comes to AGI [artificial general intelligence] and existential risk, it turns out as best I can ascertain, in the 20 years or so we've been talking about this seriously, there isn't a single model done. Period. Flat out.

So, I don't think any idea should be dismissed. I've just been inviting those individuals to actually join the discourse of science. 'Show us your models. Let us see their assumptions and let's talk about those.' The practice, instead, is to write these very long pieces online, which just stack arguments vertically and raise the level of anxiety. It's a bad practice in virtually any theory of risk communication.

And then, for some individuals, at the end of it all, you scream, 'The world is going to end.' Other people come away, 'Oh, the chance is 30% that the world will end.' 'The chance is 80% that the world will end.' A lot of people have come out and basically wanted to get rid of the U.S. Constitution: 'I'll get rid of free speech, get rid of provisions against unreasonable search and seizure without a warrant,' based on something that hasn't even been modeled yet.

So, their mental model is so much: 'We're the insiders, we're the experts.' No one is talking us out of their fears.

My mental model is: There's a thing, science. Try to publish this stuff in journals. Try to model it. Put it out there, we'll talk to you. I don't want to dismiss anyone's worries, but when I talk to people, say, who work in governments who are well aware of the very pessimistic arguments, they're just flat out not convinced for the most part. And, I don't think the worriers are taking seriously the fact they haven't really joined the dialogue yet.

• https://www.econtalk.org/tyler-cowen-on-the-risks-and-impact-of-artificial-intelligence/#audio-highlights

Recursive Structures

Physicist and Astrobiologist Sara Imari Walker wrote on X in mid 2024:

Life occurs as a continual recursive combinatorial collapse of the space of possibilities … the structures it generates are increasingly deep recursive stacks, retaining the past in the present and using this to construct the future

https://x.com/sara_imari/status/1789423907050528990?s=46&t=LeiEF5SQYzBIfYYx7cSKUw

Nudel’s summer reading list included her book on Assembly Theory, Life As No One Know it

Recursive structures are an intuitive part of the designer’s toolkit as they provide a shorter path to complexity: building components from previously constructed sub-components, embedding history into objects.

One of Nudel’s favourite smart phone Apps is a simple but clever graphic tool called Isometric. It allows for the creation of “3D” structures using only parallelograms of different colours and orientations.

Playing with this tool, users soon work out that, rather than building designs from single parallelogram placement, it is more effective to build a library of subcomponents. These then become the next generation of parts from which to build structures of greater (and recursive) complexity

According to Assembly Theory, this is precisely what biological systems have been doing for aeons

Koch, Menger, and Recursive Loops

Helge von Koch, Karl Menger, and the concept of recursive loops share deep connections through their contributions to fractal geometry. Koch, best known for the Koch Snowflake, introduced a way to create complex shapes through repeated, recursive processes.

This figure exemplifies how a simple geometric transformation can recursively generate infinitely intricate boundaries, illustrating the early ideas of fractals. Menger, inspired by similar principles, developed the Menger Sponge, a three-dimensional fractal that recursively subdivides a cube into smaller cubes. These mathematicians' work underlines the fundamental principle of recursive loops: using repeated application of a simple rule to generate complex structures, which is a cornerstone in the study of fractal geometry.

Nudel has been constructing models using ChatGPT to write Python code and the Trimesh module.  Recent experiments have focussed on fractal constructions after Koch and Menger

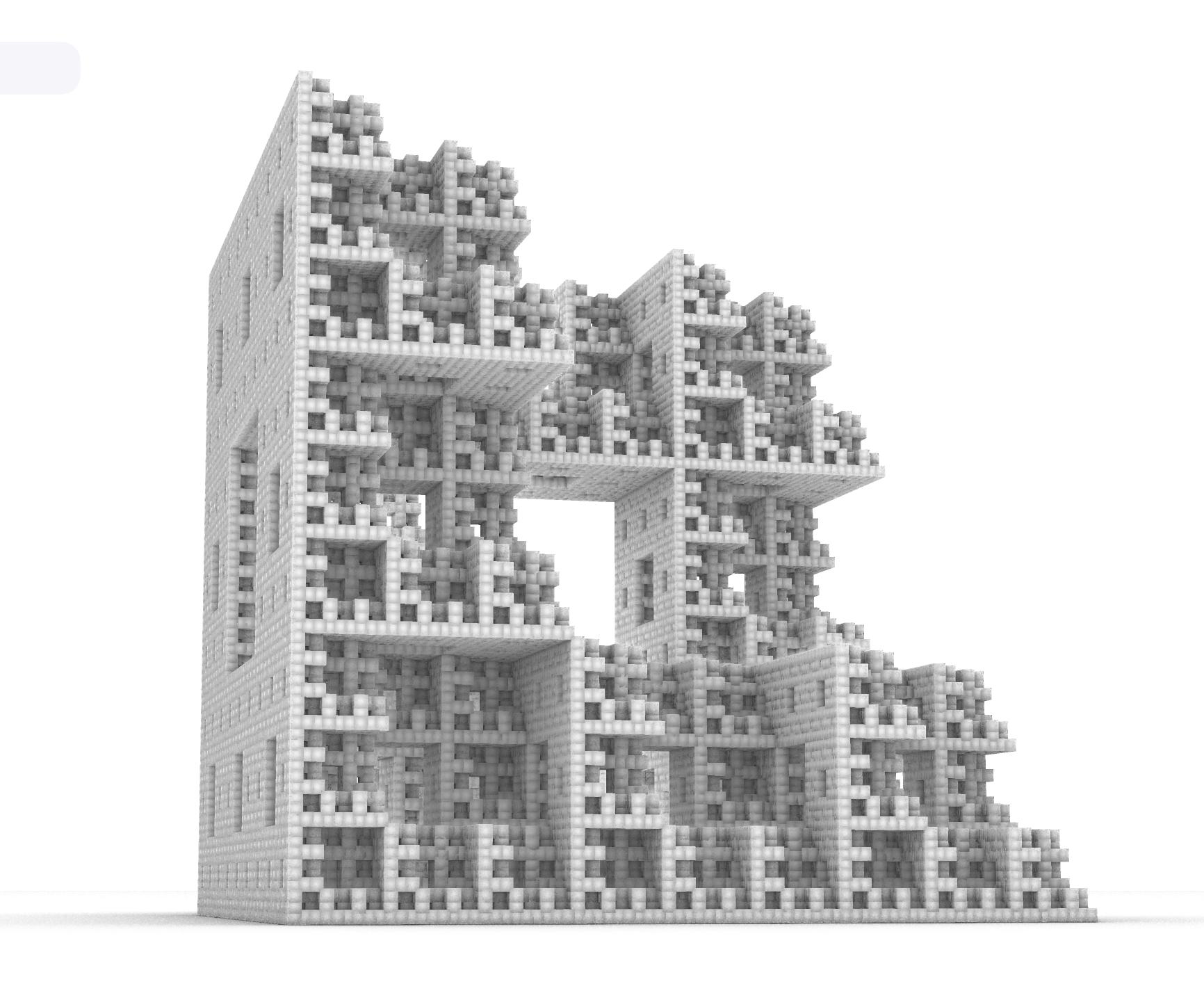
Images by Nudel

Image by Hyungsoo Kim : https://www.grasshopper3d.com/profile/HyungsooKim

Assembly Theory

One of the more tantalising quotes encountered by Nudel on Twitter in recent months was by Sara Amari Walker, theoretical physicist and astrobiologist:

Life occurs as a continual recursive combinatorial collapse of the space of possibilities … the structures it generates are increasingly deep recursive stacks, retaining the past in the present and using this to construct the future

• https://x.com/sara_imari/status/1789423907050528990?s=61

The quote encapsulates the ideas that Walker, Cronin, and others have developed via what they refer to as Assembly Theory - https://www.nature.com/articles/s41586-023-06600-9.pdf

Nudel asked ChatGPT to create a diagram that explains the quote

Economic Model by ChatGPT

“The Solow–Swan model, or exogenous growth model, is an economic model of long-run economic growth. It attempts to explain long-run economic growth by looking at capital accumulation, labor or population“

• Wikipedia

Nudel sought to test ChatGPT’s ability to build an economic model by asking:

“Build an excel file that models Solow-Swan economic growth”

Like many ChatGPT outputs, the result was interesting, but flawed:

To build an Excel model for the Solow-Swan economic growth model, we'll create a simple spreadsheet that calculates economic outputs over time based on initial conditions and assumptions of the model. The Solow-Swan model typically uses parameters like savings rate, depreciation rate, population growth rate, and the rate of technological progress. Here's how we can structure the model:

1. Parameters:

• ( s ): Savings rate

• ( n ): Population growth rate

• ( g ): Technological growth rate

• ( delta ): Depreciation rate

• ( alpha ): Capital's share of income (elasticity of output with respect to capital)

2. Initial Conditions:

• ( K_0 ): Initial capital stock

• ( L_0 ): Initial labor force

• ( A_0 ): Initial level of technology

• ( Y_0 ): Initial output, calculated as ( Y_0 = A_0 imes K_0^alpha imes L_0^{1-alpha} )

3. Yearly Calculations:

• ( A_{t} = A_{t-1} imes (1 + g) ): Technology next year

• ( L_{t} = L_{t-1} imes (1 + n) ): Labor force next year

• ( K_{t} = (1 - delta) imes K_{t-1} + s imes Y_{t-1} ): Capital stock next year

• ( Y_{t} = A_{t} imes K_{t}^alpha imes L_{t}^{1-alpha} ): Output next year

4. Output for Analysis:

• Per capita output: ( y_t = rac{Y_t}{L_t} )

• Capital per worker: ( k_t = rac{K_t}{L_t} )

Let's go ahead and set up these calculations in an Excel file. I'll create the initial structure and formulas based on typical economic growth parameters. After that, I can share the file with you.

• ChatGPT 4, May 2024

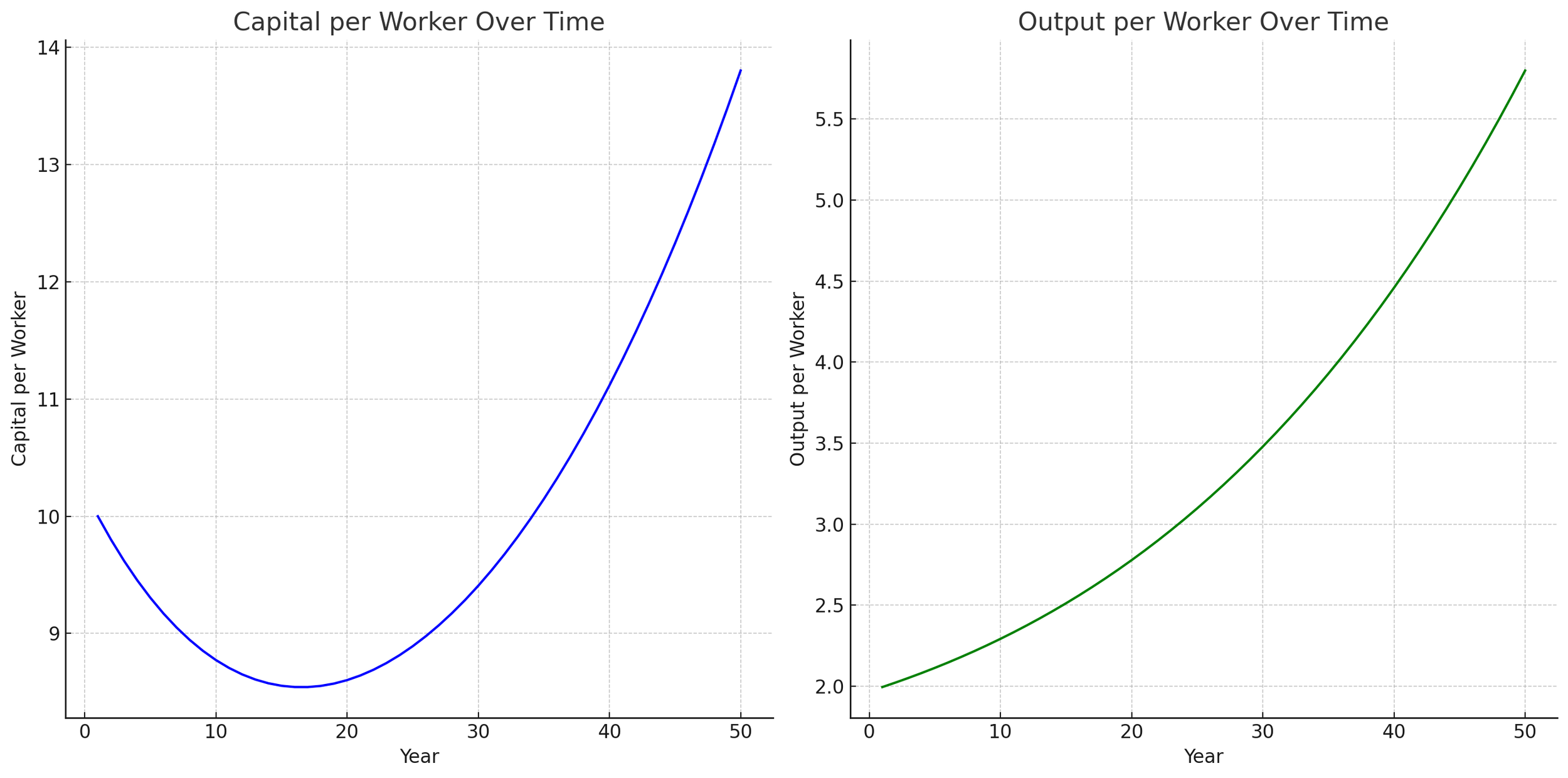
Nudel then asked ChatGPT to output plots from the Excel files resulting in the graphs above. The hockey-stick curve shown is distinctly different to the relationship expected of the Solow-Swan model whereby marginal gains in capital per capita decrease as an economy matures.

ChatGPT explained the results of its outputs from Excel as follows:

The appearance of a "hockey stick" relationship in the graph of capital per capita over time can initially seem counterintuitive given the principle of diminishing returns to capital. However, this visual trend can be explained by several factors related to the parameters and dynamics of the Solow-Swan model:

1. Accumulation Phase: Early in the development process, significant increases in capital per worker can occur because the economy is starting from a lower base of capital. This phase often shows rapid growth as initial investments yield high returns due to relatively scarce capital.

2. Compound Growth: Even with diminishing returns to capital, as long as the savings rate remains constant and above the combined rates of population growth and depreciation, the economy can still accumulate capital. The model incorporates reinvestment of a portion of output, which compounds over time, leading to a rapid increase in capital stock initially.

3. Technological Growth: The model you've seen also includes technological progress, which enhances the productivity of both capital and labor. Technological growth can offset some of the diminishing returns to capital by effectively increasing the output generated from existing levels of capital and labor.

4. Transition to Steady State: Over a longer period, the economy should approach a steady state where the rate of capital accumulation aligns more closely with the rates of population growth and depreciation. In the steady state, increases in capital per worker taper off, and any further growth in output per worker is primarily due to technological advancements rather than capital deepening.

The "hockey stick" growth might be more pronounced depending on the initial conditions (like a very low initial capital per worker) and the specific parameter values for savings, depreciation, population growth, and technological progress. If the model's assumptions were altered (e.g., a lower savings rate or higher depreciation), the curve might flatten earlier or rise less steeply. This shape underscores how sensitive the model's outcomes can be to its input parameters.

Auxetic Foam

Auxetic foams counter-intuitively expand (shrink) under stretching (compression). These foams can exhibit superior mechanical properties such as resistance to shear and indentation, improved toughness and energy absorption (EA) under several types of loadings.

Inspired by the work of Professor Mike Xie and peers at RMIT’s Centre for Innovative Structures and Materials, Nudel has created models of large scale auxetic foam elements, rendered below as large sculptural voxels in the landscape

Examples of Auxetic Foams

Dyson Sphere Variants

From one model to the next (using a model)

Nudel has rebuilt our earlier Freeman-Dyson Earth images using Midjourney, an online generative Machine Learning tool available on the Discord platform. Midjourney can take image inputs, combined with new text prompts, to generate new images - using a model to create new models. Generative AI tools have garnered significant public attention since the release of ChatGPT in late 2022 and, more recently, the release of Google Bard in mid 2023. These AI systems are classed as LLM’s (Large Language Models).

A large language model (LLM) is a type of artificial intelligence (AI) algorithm that uses deep learning techniques and massively large data sets to understand, summarize, generate and predict new content. The term generative AI also is closely connected with LLMs, which are, in fact, a type of generative AI that has been specifically architected to help generate text-based content.

Over millennia, humans developed spoken languages to communicate. Language is at the core of all forms of human and technological communications; it provides the words, semantics and grammar needed to convey ideas and concepts. In the AI world, a language model serves a similar purpose, providing a basis to communicate and generate new concepts.

The first AI language models trace their roots to the earliest days of AI. The ELIZA language model debuted in 1966 at MIT and is one of the earliest examples of an AI language model. All language models are first trained on a set of data, and then they make use of various techniques to infer relationships and then generate new content based on the trained data. Language models are commonly used in natural language processing (NLP) applications where a user inputs a query in natural language to generate a result.

An LLM is the evolution of the language model concept in AI that dramatically expands the data used for training and inference. In turn, it provides a massive increase in the capabilities of the AI model. While there isn't a universally accepted figure for how large the data set for training needs to be, an LLM typically has at least one billion or more parameters. Parameters are a machine learning term for the variables present in the model on which it was trained that can be used to infer new content.

• https://www.techtarget.com/whatis/definition/large-language-model-LLM

Dyson Sphere for Earth

American-English physicist Freeman Dyson speculated on mega-structures encapsulating a star that could harvest all the energy output of its host : the Dyson Sphere

Nudel has speculated at the planetary scale, inspired by terraforming descriptions of otherwise inhospitable planets in Kim Stanley Robinson’s 2312: gigantic sun shading screens covering an entire planet

Based on Uber’s H3 geospatial indexing system, Nudel created a hexagonal mega grid laid across the face of the Earth

TB10_284 2022_11_01 GE - Geodesic_122_R6375_GEOD122_2-002_crop.jpg

TB10_284 2022_09_25 GeoHex Gridded Sphere - Geodesic_122_R6375_01-004_crop.jpg

TB10_284 2022_09_25 GeoHex Gridded Sphere - Geodesic_122_R6375_01-001_crop.jpg

C:\Users\black\Documents\_TB_Google_DRV\_TB_Google_Working_Files\TB10_284 2023 Rhino General\TB10_284 2022_08_27 Geo-Earth Energy Tool\TB10_284 Uber H3 Blog Post Images Nudel\TB10_269 GeoHex Gridded Sphere - Dodecahedron Axes Array_09_crop.jpg

Flat pack of 122 sided Goldberg Polyhedron

Unlike Buckminster Fuller’s Dymaxion mapping (and Uber’s H3 System too), Nudel’s works off a conventionally aligned Icosahedral Goldberg Polyhedron with a pentagon at the poles and one at zero latitude and zero longitude

Flat Pack Brain

Nudel has been digesting further the morphology of the brain via a paper in the Journal of Neuroscience: Structural and Functional Analyses of Human Cerebral Cortex Using a Surface-Based Atlas

Nudel’s interest in the neocortex was first piqued by Jeff Hawkins book One Thousand Brains

The Journal of Neuroscience paper describes a basis for determining the surface area of the brain using geometric methods to “unfold” the complex surface of the neocortex to create a map

Human cerebral cortex is a thin sheet of tissue that is extensively convoluted in order for a large surface area to fit within a restricted cranial volume.

The paper also describes several means for mapping the surface of the neocortex

Nudel’s own folded plane model provides a high level abstraction of the brain’s surface that correlates well with the surface area estimate provided in the Journal of Neuroscience paper:

• Nudel - 1365 cm3

• JoN - 1579 cm3

Use your Nüdel!

UK's Globe and Mail website has an article dating back to 2012 on the origins of the phrase "use you noodle".  Interestingly, the article also cites the use of "noodle" as a verb for free-form creativity, or to noodle around:

"To noodle around on something, while it does make use of the noodle (head), may derive from the regional German nudeln, to improvise a song, or from the late-19th-century Scottish sense of noodling as humming a song to oneself. By 1937, to noodle was to fool around with notes to create music. By 1942, perhaps by association with the doodle (a loose, free-associating drawing), it acquired the broader sense of messing about with words or ideas without a clear goal."

http://www.theglobeandmail.com/arts/books-and-media/language-use-your-noodle-old-bean/article4381047/

Human Brain Surface Area

Nudel has been modelling the human brain, using an ellipsoid set in a tilted plain as a suitable abstraction:

The resulting form has ellipsoid dimensions of 190 x 140 x 150 mm at an angle of 10 degree tilt, giving a resultant volume of 1.8 x 10^6 cubic mm. This brain study is based on the large scale head model made available from the US National Institute for Occupational Safety and Health (NIOSH).

This model also results in a surface area of 75,000 sq mm - comparable to the estimated 150,000 sq mm in the Journal of Neuroscience (Journal of Neuroscience 15 September 1997, 17 (18) 7079-7102; DOI: https://doi.org/10.1523/JNEUROSCI.17-18-07079.1997)

https://www.cdc.gov/niosh/data/datasets/rd-10130-2020-0/default.html

https://www.jneurosci.org/content/17/18/7079

3 arcing Miura surfaces were overlaid on the top of the brain to demonstrate a further abstracting of the folding form of the neocortex surface and show how this folding achieves an efficient packing of surface into the constraints of the skull

Neocortex Surface Topology & ChatGPT

Nudel’s post from September 2022 observed the similarities between the surface of the brain’s outer shell, the neocortex, and 3-dimensional folded origami surfaces (such as the Miura fold).

Nudel consulted OpenAI’s ChatGPT to see how an LLM (Large Language Model) might respond to the speculation that the folding form of the neocortex’s surface allows for a large surface area to be accommodated within the confines of the human skull. Here’s what ChatGPT had to say:

The folding of the human neocortex, or the outer layer of the cerebrum, is thought to be an adaptation that has allowed for the expansion of brain surface area within the constraints of the skull. This expansion has allowed for the evolution of increased cognitive abilities such as language, abstract thought, and consciousness.

The folded topology of the neocortex allows for a greater surface area to be packed into a smaller volume, much like how the wrinkles on a brain allow for more gray matter to be packed into the skull. The folds, or gyri, and grooves, or sulci, of the neocortex are thought to have developed as a result of the growth and expansion of the brain during development.

The folding of the neocortex is not unique to humans and is also seen in other primates and some mammals. It is thought that the more highly developed the neocortex is in a species, the more highly folded it will be.

Nudel tested the folding efficiency of a regular Miura fold plane composed of equilateral parrallelograms

Goldberg Coexter Geodesics

Nudel has been experimenting with Goldberg Coexter Construction (GC Construction) of polyhedron face subdivision

The GC construction is primarily studied in organic chemistry for its application to fullerenes,[1][2] but it has been applied to nanoparticles,[3] computer-aided design,[4]basket weaving,[5][6] and the general study of graph theory and polyhedra

GeoSpatial Indexing - Work in Progress

The Australian Bureau of Statistics (ABS) provides spatial data covering a wide range of statistical, temporal, and spatial data, including geospatial:

https://www.abs.gov.au/statistics/standards/australian-statistical-geography-standard-asgs-edition-3/jul2021-jun2026/access-and-downloads/digital-boundary-files

Nudel recently downloaded the Australia - 2021 - Shapefile and imported this into QGIS to convert to a 3-dimensional view of Australia

The shape file was then exported from QGIS as a DXF file and imported into Rhino, with a Lat\Long grid overlaid

A Grasshopper script was used to simplify the outline curve and export the points to a coordinate table in Excel - these curves were then rebuilt in Rhino, representing various levels of abstraction

The abstracted dataset comprising 65 Lat\Long pairs was then reconstructed on the sphere using polar coordinate conversion in Grasshopper

This geodesic outline can then be projected to the plane from the approximate centroid of the Australian continent (at Lat -25 / Long 135) to get a minimally distorted projection

AI Generative Design & Deep Fakes

Nudel has been playing with some of the recently released text-to-image AI platforms including

- Midjourney

- Stability

• - OpenAI’s DALL-E

One of the best explanations of the recent crop of AI work comes fro

https://podcasts.apple.com/au/podcast/techstuff/id282795787?i=1000580717767

The podcast highlights a real-time application of DeepFake technology in a recent episode of Americas Got Talent with the mapping of judges faces on a trio of performers singing Puccini’s Nessun Dorma

Simon, Terry, and Howie Sing "Nessun Dorma" on Stage?! Metaphysic

Models : Cognition / Research / Design

Models are a key focus of Nudel’s research program as they relate to cognition, research, and design.

Definition of a Model

There are many definitions of the word model. The following definitions refer to a model as a representation of selected aspects of a domain of interest to the modeler:

• a physical, mathematical, or otherwise logical representation of a system, entity, phenomenon, or process (DoD 1998);

• a representation of one or more concepts that may be realized in the physical world (Friedenthal, Moore, and Steiner 2009);

• a simplified representation of a system at some particular point in time or space intended to promote understanding of the real system (Bellinger 2004);

• an abstraction of a system, aimed at understanding, communicating, explaining, or designing aspects of interest of that system (Dori 2002); and

• a selective representation of some system whose form and content are chosen based on a specific set of concerns; the model is related to the system by an explicit or implicit mapping (Object Management Group 2010).

.Nudel deploys models as a mode of research - a means of exploration/analysis/design through construction.

The images below were constructed in Rhino/Grasshopper as a means to understanding the scale of the brain, in particular the surface area of the neocortex that comprises:

a set of layers of the mammalian cerebral cortex involved in higher-order brain functions such as sensory perception, cognition, generation of motor commands, spatial reasoning and language.

The neocortex is smooth in rodents and other small mammals, whereas in elephants, dolphinsand primates and other larger mammals it has deep grooves (sulci) and ridges (gyri). These folds allow the surface area of the neocortex to be greatly increased. All human brains have the same overall pattern of main gyri and sulci, although they differ in detail from one person to another.

An MRI study of 46 adults of mainly European descent found that the average male had a brain volume of 1,274 cubic centimeters (cm3) and that the average female brain measured 1,131 cm3

Could this folded topology of the neo-cortex sulci and gyri be modelled as a folded plane, borrowing from a modular origami system, such as Miura-ori

Geospatial Indexing with Hexagonal Sphere Divisions

Nudel has been playing with hexagonal sphere divisions, based primarily on Uber’s H3 geospatial indexing system

Uber’s H3 geospatial indexing system

The Uber H3 system relies on a global division that starts with the spherical projection of a 122-sided polyhedron comprising 12 pentagons and 110 hexagons, a type of Goldberg Polyhedron. Uber’s system rotates the sphere so that the pentagons avoid major land areas

Nudel’s mapping deploys the same Goldberg Polyhedron spherical projection conventionally oriented

120 sided polyhedron

Nudel’s interest in Geospatial Indexing is part of a broader research program focussed on models

Earth with conventionally oriented Goldberg Polyhedron
{5+,3}2,2 - TB10_284 2022_09_25 GeoHex Sphere_122_R6375._001

BooleanBoxCross

Nudel has been busy on a number of commissioned pieces for private collectors and corporate clients with 2 major installations due for completion in February 2016  

The BooleanBoxCross is a prototype of a foyer installation for a boutique hedge fund in Melbourne 

Generative Art 01

Using the Processing language, Mark Nystrom has taken data streams of complex natural phenomenon from a number of sources to produce a series of striking visualizations;

http://www.marknystrom.com/

Digital Clouds

In the search for graphic coding systems, Nüdel came across the work of Dutch Master, Karel Martens. Martens work includes commercial wall fabric designs for Maharam. Based on the deconstruction of a photograph of clouds, taken on the day of his Grandson's birth, Martens reimagines the Pixel;

http://www.maharam.com/collaborators/martens-karel